
Variable aleatoria continua
Hanwen Zhang, Ph.D.
2022-II
Variable aleatoria continua
Una variable aleatoria es continua si toma valores en un intervalo
Una v.a. continua toma infinitos valores.
El intervalo puede ser de forma (a,b), [a,b], (−∞,a), (b,∞), entre otros.
Ejemplo: Y denota el precio de dólar de mañana: Y puede tomar cualquier valor entre: 800 pesos chilenos y 900 pesos chilenos.
Ejemplo: Z denota los cambios de un índice bursátil, Z puede tomar cualquier valor entre: -15% y 20%.
Comportamiento de una v.a. continua
No se puede conocer de antemano el valor que vaya a tomar una v.a., pero sí podemos calcular las probabilidades.
Estas probabilidades se representan por medio de la función de densidad f(x).
En la gráfica de f(x), los valores de la variable están en el eje horizontal, los valores de f(x) están en el eje vertical.
Función de densidad continua

Función de densidad continua

Función de densidad continua

Función de densidad continua
En general, para una v.a. continua X, la función de densidad f(x) cumple:
- f(x)≥0
- ∫∞−∞f(x)dx=1 (el área bajo la curva de la función f(x) es 1)
Función de densidad continua

Función de densidad continua

Función de densidad continua

Uso de f(x) continua
Pr(a<X<b)=∫baf(x)dx=Área bajo curva de f(x)

Uso de f(x) continua

Uso de f(x) continua

Uso de f(x) continua
Ejercicio 1. Para esta función de densidad, represente gráficamente las siguientes probabilidades:
- Pr(X>5)
- Pr(1<X<4)
- Pr(X<8)
- Pr(X=1)
Uso de f(x) continua
Ejercicio 2. Para la siguiente función de densidad donde los diferentes valores indica áreas correspondientes

Uso de f(x) continua
- Expresar los 4 valores en términos de las probabilidades:
- 0.16=Pr()
- 0.34=Pr()
- 0.48=Pr()
- 0.02=Pr()
- Calcular las siguientes probabilidades:
- Pr(X<0)=
- Pr(X>0)=
- Pr(X<2)=
- Pr(X>−1)=
- Pr(−1<X<2)=
Interpretación de f(x)
Densidad de la variable ingreso mensual por persona: Línea verde (país A), línea azaul (país B)

Interpretación de f(x)
- Se puede ver que la mayoría de las personas del país A tienen ingreso entre 500 y 1500 pesos. ¿Qué se puede decir del país B?
- ¿Si una persona con ingreso menos de 1000 dólares mensuales se clasifica como pobre, en qué país hay más pobres?
- En qué país hay mayor porcentaje de personas con ingreso mayor a 2500 dólares mensuales?
- ¿En general cuál país tiene mayor ingreso?
Distribución uniforme continua
Una v.a. continua tiene distribución uniforme sobre un intervalo (a,b) si su función de densidad está dada por f(x)={1b−asi a<x<b0si no
La función de densidad es una constante, y su gráfica es una línea horizontal en el intervalo (a,b).
Se usará la notación X∼Unif(a,b).
Distribución uniforme continua
Diferentes distribuciones exponencial.

Distribución Exponencial
Una v.a. continua X tiene distribución exponencial con parámetro de escala θ>0 si su función de densidad está dada por: f(x)={1θe−xθsi x>00si no
Se usará la notación X∼Exp(θ).
Distribución Exponencial
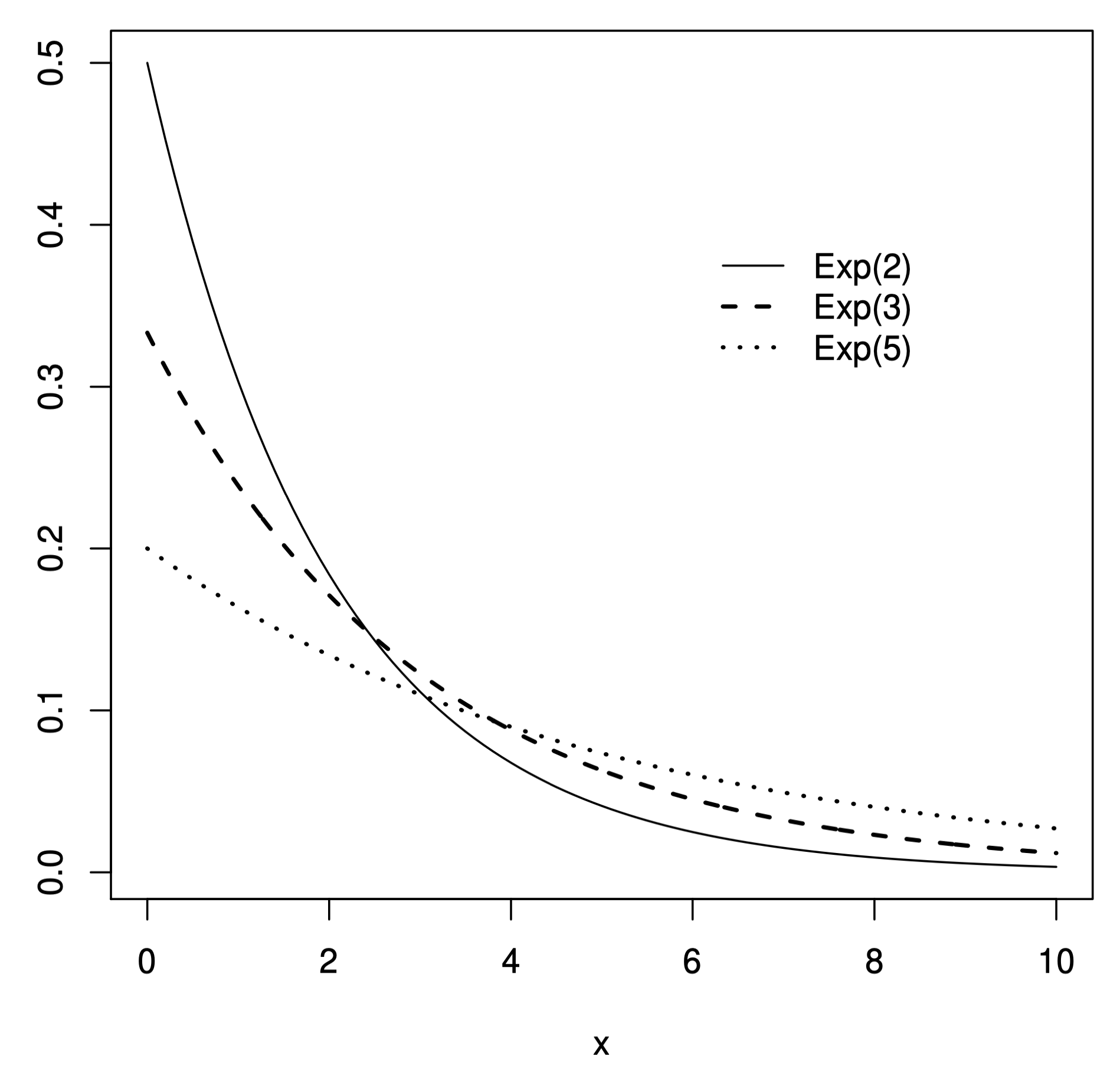
Uso de Distribución Exponencial
La distribución exponencial toma valores positivos, y puede ser utilizado para describir el tiempo necesario para la ocurrencia de algún evento.
Ejemplo: tiempo de sobrevivencia de pacientes, la vida útil de algún equipo.
En la anterior gráfica, se puede ver que la distribución Exp(2) está más concentrada en valores pequeños de X, comparada con Exp(3) y Exp(5).
En Exp(θ), entre menor sea θ, más tiende X a tomar valores pequeños.
Distribución Exponencial
Comparación de f(x) para la vida útil (en años) de dos marcas de lavadoras (marca verde y marca azul)

- ¿Cuál lavadora tiene mayor probabilidad de dañar antes de 3 años?
- ¿Cuál lavadora tiene mayor probabilidad de durar más de 10 años?
- ¿Cuál lavadora es mejor en términos de duración?
Distribución Exponencial
Propiedades: Si X∼Exp(θ) entonces
E(X)=θ
Var(X)=θ2
La esperanza de la distribución coincide con el parámetro θ. Por lo tanto, entre menor sea θ, más tiende X a tomar valores pequeños.
Distribución Exponencial
Suponga que X denota el tiempo transcurrido entre 2 temblores en Chile, y X∼Exp(θ=3.5 meses), y Y denota la misma variable para Colombia con Y∼Exp(θ=6.7 meses).
En una misma gráfica representa la función de densidad de X y Y.
Probabilidades de Exp(θ)
Recuerden: Pr(a<X<b)=∫baf(x)dx

Ejercicio Exp(θ)
Suponga que X denota la vida útil de una cierta marca de lavadora, y X∼Exp(θ= 5.7 años).
¿En promedio cuánto tiempo dura una lavadora de esta marca?
¿Cuál es la probabilidad de que una lavadora de esta marca dure menos de 3 años?
¿Cuál es la probabilidad de que una lavadora de esta marca dure más de 10 años?
Usted compra una lavadora de esta marca usada con 3 años de uso, ¿cuál es la probabilidad de que dure 4 años más?
Ejercicio Exp(θ)
- ¿En promedio cuánto tiempo dura una lavadora de esta marca?
E(X)=?
Respuesta: En promedio una lavadora de esta marca dura 5.7 años, esto es, aproximadamente 5 años y 8 meses.
Ejercicio Exp(θ)
- ¿Cuál es la probabilidad de que una lavadora de esta marca dure menos de 3 años? Pr(X<3)
En Excel, usar la función EXPON.DIST

Respuesta: La probabilidad de que una lavadora de esta marca dure menos de 3 años es de 40.92%.
Ejercicio Exp(θ)
- ¿Cuál es la probabilidad de que una lavadora de esta marca dure menos de 3 años? Pr(X<3)
Ejercicio Exp(θ)

Ejercicio Exp(θ)
- ¿Cuál es la probabilidad de que una lavadora de esta marca dure más de 10 años?
Pr(X>10)=1−Pr(X<10)

Respuesta: la probabilidad de que una lavadora de esta marca dure más de 10 años es de 17.30%.
Ejercicio Exp(θ)
- ¿Cuál es la probabilidad de que una lavadora de esta marca dure más de 10 años?
Pr(X>10)=1−Pr(X<10)
Ejercicio Exp(θ)

Ejercicio Exp(θ)
- Usted compra una lavadora de esta marca usada con 3 años de uso, ¿cuál es la probabilidad de que dure 4 años más?
Pr(X>7|X>3)=Pr(X>7 y X>3)Pr(X>3)=Pr(X>7)Pr(X>3) =0.29290.5908=0.4957=49.57%
Distribución Normal
Dentro de todas las distribuciones de probabilidad, la más importante es la distribución normal.
- Presentada por primera vez en el 1733.
- También conocida como la distribución gaussiana por el matemático, físico y astrónomo Carl Friedrich Gauss. (https://es.wikipedia.org/wiki/Ley_de_Stigler).
- Tiene muchas propiedades que otras distribuciones no tienen.
- La mayoría de modelos estadísticos se formulan primero para la distribución normal, y después se extiende a las otras distribuciones.
Distribución Normal
Una v.a. X sigue una distribución normal con parámetros μ y σ2 si su función de densidad está dada por: fX(x)=1√2πσ2exp{−12σ2(x−μ)2} donde σ>0.
- X toma valores desde −∞ hasta ∞
- Notación: X∼N(μ,σ2).
Distribución Normal

Densidad Normal
La forma de la función de densidad es definida por los dos parámetros: μ y σ

Distribución Normal
μ corresponde al eje de simetría de f(x)

Distribución Normal
La mayor probabilidad está concentrada alrededor de μ.

Distribución Normal
Propiedad de la distribución X∼N(μ,σ2):
E(X)=μ
Distribución Normal
El segundo parámetro σ determina qué tan concentrada está la variable alrededor de μ.

Distribución Normal
En ambas gráficas, los valores de X están concentrados alrededor de 1, pero los de σ=1 están más concentrados que σ=2

Distribución Normal
Propiedad de la distribución X∼N(μ,σ2):
Var(X)=σ2 Entre más pequeño sea σ, más concetrados están los valores de X alrededor de μ.
Ejemplo Normal
Suponga que el número de ventas diarias de un almacén sigue la distribución N(μ=23, σ=5)
La función de densidad es:

El número promedio de ventas diarias es de 23 ventas.
La diferencia promedia entre distintos días es de aproximadamente 5 ventas.
Probabilidades Distribución Normal
Pr(a<X<b)=Área bajo curva de f(x)
Pr(a<X<b)=∫baf(x)dx=∫ba1√2πσ2exp{−12σ2(x−μ)2}
Este integral no tiene solución analítica, sino que se calcula con métodos numéricos (aproximaciones).
Ejemplo Normal
Suponga que el número de ventas diarias de un almacén sigue la distribución N(μ=23, σ=5), calcular probabilidad de que en un día determinado
- haga menos de 10 ventas
- haga más de 30 ventas
- haga entre 10 y 40 ventas
Ejemplo Normal
X denota el número de ventas en un día, entonces X∼N(μ=23, σ=5) ó X∼N(μ=23, σ2=25)
- Probabilidad de que en un día determinado haga menos de 10 ventas: Pr(X<10)
En Excel, usar la función NORM.DIST

Ejemplo Normal
En R, usar la función pnorm
Ejemplo Normal
- probabilidad de que en un día determinado haga más de 30 ventas: Pr(X>30)=1−Pr(X<30)
En Excel,

Ejemplo Normal
En R,
Ejemplo Normal
- Probabilidad de que en un día determinado haga entre 10 y 40 ventas: Pr(10<X<40)=Pr(X<40)−Pr(X<10)
En Excel,

Ejemplo Normal
En R,
Ejemplo Normal

Distribución Normal Estándar
En una distribución normal, cuando μ=0 y σ=1, la distribución se conoce como la distribución Normal Estándar. (Z∼N(0, 1))

Distribución Normal Estándar
Cualquier distribución normal se puede convertir a una distribución normal estándar (estandarización)
Si X∼N(μ,σ2), entonces Z=X−μσ∼N(0, 1)
Antiguamente, el cálculo sobre cualquier distribución normal se realiza por medio de la N(0,1).
Distribución Normal Estándar
Existen 3 tipos “tablas” de la distribución normal estándar que permiten cálculo de probabilidades:
- probabilidades acumuladas
- probabilidades complementarias
- probabilidades acumuladas desde la media
Tabla Normal Estándar (probabilidades acumuladas)

Los valores de tabla corresponden a Pr(Z<z).
Pr(Z<−2.14)=0.0162=1.62%
Pr(Z<−0.8)=0.2119=21.19%
Pr(Z<−1.35)=??
Pr(Z<0.92)=??
Tabla Normal Estándar (probabilidades complementarias)

Los valores de tabla corresponden a Pr(Z>z)
Pr(Z>1.23)=0.1093 Pr(Z>−0.75)=1−0.2266=0.7734 Pr(−0.35<Z<0.66)=??
Tabla Normal Estándar (probabilidades acumuladas desde la media)

Los valores de tabla corresponden a Pr(0<Z<z)
Pr(0<Z<1.35)=0.4115 Pr(0<Z<0.72)=0.2642 Pr(0<Z<0.66)=?? Pr(Z<1.36)=?? Pr(Z<−0.52)=?? Pr(Z>1.03)=?? Pr(Z>−0.93)=??
Probabilidades en Distribución Normal
Ejemplo: Suponga que el número de ventas diarias de un almacén sigue la distribución N(μ=23, σ=5), calcular probabilidad de que en un día determinado
- haga menos de 10 ventas
- haga más de 30 ventas
- haga entre 10 y 40 ventas
Probabilidades en Distribución Normal
X∼N(μ=23, σ=5)
Pr(X<10)=?? Pr(X<10)=Pr(X−235<10−235)=Pr(Z<−2.6)=0.0047
Pr(X>30)=??
Probabilidades en Distribución Normal
En una distribución N(μ,σ2) Pr(μ−2σ<X<μ+2σ)=Pr(−2<Z<2)≈95%
Con probabilidad 95%, los valores de una v.a. normal está alrededor de su media μ más y menos 2 desviaciones.
Probabilidades en Distribución Normal
Ej: Número de ventas diarias ∼N(μ=23,σ=5), entonces con probabilidad 95%, se vende diariamente entre 23−2∗5=13 y 23+2∗5=33 libros
Ej: El precio de boleta de avión desde Santiago a Bogotá ∼N(μ=1500USD,σ=400USD), entonces con probabilidad 95%, el precio está entre _______ USD y ______ USD
Percentiles normal
Definición: el percentil p de una distribución es el valor de la variable que tenga probabilidad acumulada (hacia la izquierda) p.

Percentiles normal
El concepto de los percentiles es muy importante en la estadística, porque se usan en diferentes cálculos casi todas las ramas de la estadística.
Percentiles de la N(0,1)
En Excel: usar la función NORM.S.INV

Percentiles normal
Percentiles de la N(0,1)
En R: usar la función qnorm:
Decimos que 1.96 es el percentil 97.5% de la distribución N(0,1)
z0.975=1.96
¿Con probabilidad ___%, la Z está entre -1.96 y 1.96?
Percentiles normal
Encuentra los percentiles 50% y 95% de la distribución N(0,1).
z = z =
Percentiles normal
Percentiles de cualquier normal
En Excel: usar la función NORM.INV.
Percentil 97.5% de la distribución N(μ=23,σ=5)

Percentiles normal
Percentiles de cualquier normal